Connecting the dots: A look into applications of graph theory 

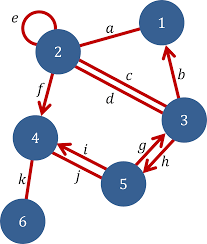
At first glance, graphs are collections of nodes, or vertices, connected by lines, or edges. Although visually simplistic, they are surprisingly useful as tools, especially in machine learning. As Frank Harary, a founder of The Journal of Graph Theory, once wrote, “It has become fashionable to mention that there are applications of graph theory to some areas of physics, chemistry, communication science, computer technology, electrical and civil engineering, architecture, operational research, genetics, psychology, sociology, economics, anthropology, and linguistics.” Fundamentally, graphs can model any relation between objects, from websites to animal species to molecules. 

“Fundamentally, graphs can model any relation between objects.”

 

Google’s PageRank algorithm  

The Google search engine has dominated humans’ lives for decades. The key to its effectiveness is a powerful algorithm. But how does it work? And what makes it so powerful? The short answer is PageRank.  

Mathematically speaking, the algorithm is the application of Markov Chains. These are directed graphs in which two nodes are connected by arrows with values assigned to them rather than simply by lines. Each arrow’s values represent the probability of going from one node to another, and, according to the rules of probability, the sum of the values going out of each node must be 1. So, if a node has only one arrow pointed out of it, the value of its arrow must be 1. Consider a graph with nodes A, B, and C where the starting node is A. If A has arrows pointing to nodes B and C, both arrows may have probabilities of 0.5 (as 0.5 + 0.5 = 1). So, half the time, if a person is standing at node A, they will travel to node B. Similarly, half the time, they will travel from node A to C. This process of traveling between nodes can be repeated and is called a “random walk.”   

  

PageRank is a random walk on the World Wide Web graph, where the nodes are webpages and the arrows are hyperlinks. Before PageRank starts, it assigns each hyperlink with the same probability. Given n pages, each probability is 1/n. The total probability of ending on a particular page is then the number of its hyperlinks times 1/n. If a page has 6 hyperlinks, for example, the total probability is 6/n. At each step, PageRank reevaluates each probability. Thus, given a page with the most hyperlinks, the probability of ending on such a page is higher than any other page. This process is how the ranking of a page after a Google search is determined, hence the name PageRank. Explicitly, the page with the highest probability has rank 1, the second highest has rank 2, and each subsequent page is ranked according to this ordering of probabilities from highest to lowest. 

 

Phylogenetic tree reconstruction 

From the evolutionary trees in secondary school to mapping families of organisms, phylogenetic trees help explain the process of species grouping. It may be assumed that graphs can simply be used in the following way: take a group of any animal, say birds. Each bird is a node, and two birds are connected via a line if they are related. However, this representation only shows whether two birds are related and not how related they are.

As with PageRank, each line on the graph can be assigned a value. However, the graph representing phylogenetic trees is different than a Markov Chain. In this graph, the values of each line take distance, or relatedness, into account: Small values between nodes mean they are closely related, while larger values indicate they are loosely related. With the graph of the phylogenetic tree, it is then possible to construct a phylogenetic tree explicitly by finding the common ancestor of all species first and then its descendants, using normalized graph cuts.

A graph cut, as the name suggests, is the removal of a node from the graph. To determine which node to cut, each node is given a value, which is the sum of all values of lines connected to such node. The nodes are cut according to an ordering of these values from smallest to largest. The smallest value is cut first, then the second smallest, and so on. A “normalized” graph cut is different only in how the value of each node is computed. Instead of just taking the sum, the value is then divided by the total number of lines in the graph. If there are two or more nodes with the same value, then all of them are cut simultaneously. In the context of phylogenetic tree reconstruction, the first cut node is the common ancestor, the second cut node is its direct descendant, and each subsequent cut node is the direct descendant of the previous. 

 

Protein-protein interactions networks  

Proteins interact with other proteins. By studying protein-protein interactions (PPIs), scientists seek to better understand their behavior and their roles collectively. Graphs can be used to model the disassortative or assortative nature of the PPI networks, which is to say how the PPI networks are organized. Disassortative PPI implies that the proteins involved are genetically dissimilar, while assortative PPI implies that they are genetically similar. 

  

The “assortativity” of a graph refers to how nodes connect to one another based on their properties. Assortative graphs have nodes that connect to each other if they have similar properties. Conversely, disassortative graphs have nodes that connect to each other if they have dissimilar properties.  In this setting, each node is a protein. If they interact, then they are connected via lines. For assortative graphs, nodes tend to form one collective hub. For disassortative graphs, nodes are found in different groupings or clusters. As PPI networks are thought to be more disassortative than assortative, graphs may help study the complexity of these proteins.

In this setting, each node is a protein. If they interact, then they are connected via lines. For assortative graphs, nodes tend to form one collective hub. For disassortative graphs, nodes are found in different groupings or clusters. As PPI networks are thought to be more disassortative than assortative, graphs may help study the complexity of these proteins.  

***

These applications are among a few in a myriad of uses for graphs. Yet they can model any relationship between objects. Moreover, they are very visual, providing insights into how they work. As a field of study, graph theory speaks to the omnipresent aspect of mathematics; the fact that it is universal in its power to describe and study the world.